这篇东西其实是本科上《机械振动》这门课的时候写的课程大作业,当时老师给了几个题目,这个还挺有意思。前几天在网盘里无意中看到了,就发上来吧。那个时候写的课程作业格式也不太规范,有的图和引用当时也没有记录来源,可能有的理解不完全正确,现在也没有再继续了解过关于振动的相关知识了。凑活一看。
————————————————————————
本文第一部分是关于小提琴相关构造的一些介绍。第二部分探究了小提琴的发声原理以及琴弦的振动模型,得到了影响琴弦固有频率的因素。接下来第三章用数学和振动相关知识解释了关于音律背后的理论依据,而且对小提琴调音过程中常提到的关于双音和谐做了简单的直观的解释。最后介绍了小提琴调音的过程,并根据前面探究过的纯五度和同度和谐以及调音操作做了详细的理论解释。
小提琴的构造与发声过程
————————————————————————
小提琴属于四弦的弓弦乐器,是现代管弦乐团弦乐组中最重要的乐器,一般在管弦乐作品中会分成第一小提琴与第二小提琴两个声部。作为现代弦乐器中最具分量的乐器,小提琴主要的特点在于其辉煌的声音、高度的演奏技巧和丰富、广泛的表现力。又被称作为乐器中的女王。
小提琴包括琴身(包括琴头、琴颈、指板和共鸣箱)、琴弦系统(包括弦轴、挂弦板、琴马和琴弦)和琴弓。琴身为木制结构,以槭木和云杉为原材料配合制造的音色最佳;琴弦一般为金属丝,也有一部分是的合成纤维和羊肠材料;琴弓由马尾毛制成。下图为小提琴结构图片[1]:
小提琴由许许多多的零件构成,可以说是“麻雀虽小,五脏俱全”。小提琴的发音来源于用弓拉琴弦,再通过琴码传递振动给共鸣箱。琴弦和琴码的制作材料、安装位置、振动特性等因素对小提琴的发音起着决定性的作用。
小提琴拉弦或拨弦使琴弦发生振动,振动由琴码传到琴身面板。琴身内部的空气藉此产生振动而共鸣发声,将振动放大后通过空气传至人耳,人耳便可听到优美的乐声。
四条琴弦自小提琴的底部延伸,跨过琴马,至指板尾端以弦轸固定。调音方法是扭动弦轸以调整琴弦的松紧。
小提琴琴弦的振动分析
————————————————————————
自激振动[2]
自激振动的物理解释:存在一个与系统有关的外部恒定的能源,自激振动靠系统外部能源补充能量,使运动的系统与恒定能源之间产生交变力,这个交变力在运动方程中体现为阻尼项。当系统振动较小时,方程中的阻尼阻尼项成为负阻尼,使系统周期性地从恒定能源吸收能量而使运动增长;当运动增长到一定程度,方程中地阻尼项成为正阻尼而使运动衰减。当系统在一个周期内损失的能量和吸入的能量相等时,系统呈现稳态的周期运动。这种稳态周期运动就成为自激振动,或简称自振。
自激振动由于能源恒定而不同于强迫振动。系统依靠自身运动状态的反馈作用调节能量输入,以维持不衰减的持续振动。也就是说,在自激振动中,外界恒定的能源给予振动系统的交变力是由运动本身产生或控制的,运动一旦停止,交变力也随之消失。而在强迫振动中,交变力是由外部能源独立产生的,它不依赖于运动,即使运动消失了,交变力仍可存在。因此,强迫振动的频率完全决定于外加激励频率,而自激振动的频率则很接近于系统的固有频率。另外,自激振动与保守系统的自由振动也不相同。保守系统的自由振动的振幅由初始条件确定,而自激振动的振幅与初始条件无关,它决定于系统本身的参数。
小提琴琴弦的振动就属于自激振动的范畴,琴弓的拉动为琴弦的振动提供连续不断的能源,使琴弦发出稳定、持续、响亮的声音。
小提琴琴弦的振动分析
琴弓与琴弦之间的相互作用可以用“黏滑”来描述:当琴弦与琴弓的速度相等时,就与琴弓黏在一起做匀速运动;当琴弦的弹性恢复力增大,琴弦就往相反的方向滑动,这就是“黏滑”运动(stick-slip)。 当琴弦与琴弓“黏”在一起做匀速运动时,琴弦振动的幅值由琴弓的速度和琴弓到琴马的相对距离决定:振动幅值与琴弓的速度成正比,与琴弓到琴马的相对距离成反比(相对距离=琴弓到琴马的距离/弦长)。琴弓与琴弦之间存在干摩擦力,当琴弓通过摩擦力咬住(即黏、stick)琴弦一同向右运动时,琴弦被琴弓带动作单方向的匀速运动。随着琴弦变形的增大,弹性恢复力也不断增大,当琴弦移动到一定程度,弹性恢复力足以克服摩擦力时,琴弦即被迫脱离琴弓向左滑动,起先在弹性恢复力下加速,超过平衡位置时开始减速,直到相对速度减到等于零时,琴弦再次被琴弓咬住向右运动,这种黏着-滑动-再黏着的过程重复发生,成了周期性的运动。
实际上,琴弓奏琴时所对琴弦的驱动力也并不是恒定不变的,经过一些论文与实验验证,这个驱动力的形状是呈锯齿形的[3]。
小提琴弦的简化振动模型
小提琴弦的振动可以归为自激振动模型中,其振动频率与激励的频率没有太大关系而很大程度上接近小提琴的固有频率。而小提琴弦的弹拨振动模型是较为简单的探究小提琴弦的张力、长度、材料等等因素对小提琴琴弦振动频率影响的方法。故我们就建立连续体的弦振动模型来探究小提琴弦振动的固有频率。
设有一个根琴弦张紧于手指和琴马之间,两固定点连线方向取为$x$轴(向右为正),与$x$轴垂直的方向取为$y$轴。 弦的单位长度质量为$ρ$,在横向分布力$f\left(x,y\right)$作用下作横向振动,张力为$T\left(x,y\right)$,跨长为$L$,弦$x$处的横向位移函数为$y=y\left(x,y\right)$。
取微段弦线单元体$dx$,假设弦作微小横向振动,则由牛顿定律得:
$$ \rho dx\dfrac {\partial ^{2}y}{\partial x^{2}}=f\left( x,t\right) dx+\left( T+\dfrac {\partial T}{\partial x}\right)\sin \left( \theta +\dfrac {\partial \theta }{\partial x}dx\right) -T\sin \theta $$
考虑到微振动的假设,有:
$$ \theta \approx \sin \theta \approx \tan \theta = \dfrac {\partial y}{\partial x} $$
故有:
$$ \rho dx\dfrac {\partial ^{2}y}{\partial t^{2}}=f\left( x,t\right) dx+\left( \dfrac {\partial y}{\partial x}+\dfrac {\partial ^{2}y}{\partial x^{2}}dx\right)+\dfrac {\partial T}{\partial x}\dfrac {\partial y}{\partial x}dx+\dfrac {\partial T}{\partial x}\dfrac {\partial y}{\partial x} $$
消去相应项,并不计$dx$的二次项,两边同时除以$dx$以后,整理得:
$$ \rho \dfrac {\partial ^{2}y}{\partial t^{2}}-\dfrac {\partial }{\partial x}\left( T\dfrac {\partial y}{\partial x}\right) =f\left( x,t\right), \left(0<x<L\right) \tag{①}$$
式中,$ρ=ρ\left(x\right)$, $T=T\left(x,t\right)$, $y=y\left(x, t\right)$。
方程①为弦横向振动的偏微分方程。当然,琴弦在两端处的位移为零,即:
$$ y\left( 0,t\right) =y\left( L,t\right) =0 \tag{②}$$
通常称为边界条件。方程①和②构成了偏微分方程的边界值问题。
弦的性质可以看成是均匀的,即弦的单位长度质量$ρ(x)=ρ$,设横向位移$y(x,t)$为小量,弦内张力$T$可以视为常量,则方程①简化为:
$$ \rho \dfrac {\partial ^{2}y}{\partial t^{2}}-T\dfrac {\partial ^{2}y}{\partial x^{2}}=f\left( x,t\right) $$
如果$f(x,t)=0$,则弦的自由振动微分方程为:
$$ \dfrac {\partial ^{2}y}{\partial t^{2}}=a^{2}\dfrac {\partial ^{2}y}{\partial x^{2}} \tag{③}$$
其中$a=\sqrt {\dfrac {T}{\rho }}$。
这里$a$表示弹性波沿弦向的传播速度。通常称为波动方程。
用数学的语言讲,描述弦振动的位移函数$y(x,t)$在时间和空间上是分离的,即边界值问题的解可以写成下面的形式:
$$ y\left( x,t\right) =Y\left( x\right) F\left( t\right) \tag{④}$$
式中,$Y(x)$表示弦的振动位形,只取决于变量$x$;
$F(t)$表示弦的振动规律,只依赖于时间$t$。
将式④代入方程③,得:
$$ \dfrac {1}{F\left( t\right) }\dfrac {dF^{2}\left( t\right) }{dt^{2}}=a^{2}\dfrac {1}{Y\left( x\right) }\dfrac {d^{2}Y\left( x\right) }{dx^{2}} \tag{⑤}$$
上式左端只依赖$t$,右端只依赖于$x$,所以要使上式对任意的$t$和$x$都成立,必然是二者都等于同一常数,用$-ω^2$表示这个常数,则由方程得到如下两个方程为:
$$ \dfrac {d^{2}F\left( t\right) }{dt^{2}}+\omega ^{2}F\left( t\right) =0 $$
$$ \dfrac {d^{2}Y\left( x\right) }{dx^{2}}+\beta ^{2}Y\left( x\right) =0 $$
$$ \beta =\dfrac {\omega }{a}, (0<x<L) $$
方程③为偏微分方程,通过采用分离变量法,将其转化为两个二阶常数微分方程,一个是关于时间变量$t$的,一个是关于空间变量$x$的。
如果同步运动是可能的话,表示依赖时间的函数$F(t)$必须是简谐的。可见方程的解为:
$$ F\left( t\right) =A\sin \omega t+B\cos \omega t =c\sin \left( \omega t+\varphi \right) \tag{⑥} $$
式中,$A$,$B$(或$C$,$φ$)为积分常数,由两个初始条件$y(x,0)$和$y(x,0)$来确定。
设方程的解为:
$$ Y\left( x\right) =D\sin \beta x+E\cos \beta x \tag{⑦}$$
式中$D$,$E$为积分常数,由边界条件$y(x,t)$和$y(L,t)$来确定。由边界条件:
$$ Y(0)=Y(L)=0 \tag{(8)}$$
显然对不同的边界条件,$Y(x)$将有不同的函数形式。把边界条件式⑧代入方程⑦得
$$ E=0,Dsin \beta L=0 $$
上式中,$D=0$显然不是振动解,故$\sin \dfrac {\omega L}{a}=0$。
由此可以求得无限多阶固有频率。由上式得:
$$ \omega _{r}=\dfrac {r \pi a}{L}=\dfrac {r \pi }{L}\sqrt {\dfrac {T}{\rho }}, (r=1,2…) $$
式中,频率$\omega _{r}$称为基频,或基频率,较高次频率$\omega _{r},(r=2,3…)$称为高次谐频,高次谐频是基频波的整数倍。对应于无限多阶固有频率,有限多阶固有频率振型函数:
$$ Y_{r}\left( x\right) =\sin \dfrac {r\pi x}{L}, (r=1,2…) $$
弦对应于各阶固有频率的固有振动为:
$$ Y_{r}\left( x,t\right) =Y_{r}\left( x\right) F_{r}\left( t\right) = \left( Ar\sin \omega _{r}t+Br\cos \omega _{r}t\right) \sin \dfrac {r\pi x}{L} $$
而弦的任意一个自由振动都可以表示为这些固有振型的叠加,即有:
$$ y=\left( x,t\right) =\sum ^{\infty }_{r=1}Y_{r}\left( t\right) F_{r}\left( t\right) =\sum ^{\infty }_{r=1}\left( Arsin\omega t+Br\cos \omega t\right) \sin \dfrac {r\pi x}{L} $$
从上面的分析可以看出琴弦的基频与琴弦的长度成反比,且随着张紧力的增大而增大、随着单位长度琴弦质量的增大而减小。这也就解释了,小提琴的高音琴弦要比低音琴弦细些,且同一根琴弦,手指按压的位置越靠近琴马拉琴发出的声音越高。
对于琴弦振动高次谐频,乐理中称为泛音。每一个泛音都有自己所对应的能量范围和频率特征,泛音决定了小提琴的音量、音色以及声音的持续时间等。所以当小提琴琴弓拉动琴弦时,其产生的声音是由一群频率互为整数比的基频和其高次谐频所构成,因此我们听到小提琴的声音丰富且具有和谐感。关于基频与泛音的具体说明在第三章。
很多时候,由于振动、或者环境温度变化导致琴弦长度的变化,都会导致琴弦的张紧力发生变化。张紧力的变化就会导致琴弦的基频发生变化,就是我们常常说的“音不准”的问题。通过扭动弦轸以调整琴弦的松紧,就可以达到调音的目的。
调音的具体方法以及原理在接下来的章节解释,不过在此之前先介绍一些关于音律的知识。
音律的数学原理
————————————————————————
音律的发展与名词的解释
纯律:指两个音的声波震动的比例越单纯,则这两个音听起来会越和谐,反之则越不和谐。这也是人类耳朵天生的特性,所以早期所谓和谐音程的声波振动频率比例大致如下:
| 音级 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | $\dot{1}$ |
|---|---|---|---|---|---|---|---|---|
| 频率比 | 1 | 6/5 | 5/4 | 4/3 | 3/2 | 5/3 | 8/5 | 2 |
虽然纯律最符合人类耳朵对美声的要求,能够有非常优美的和声音响效果,但却不太实用。因为这样的比例会因为转移调性而有很大的麻烦,例如C大调的主音是DO,应该以DO为起点,依照比例而定出其他音的音高,但如果转到G大调,所有的音的音高就会稍微做一些改变了。
十二平均律:随着音乐的发展,纯律的缺点就显示出,为了解决这问题,十二平均律应运而生。将一个纯八度(如c1—c2)平均分成十二个均等的部分——半音,这种定律法就叫“十二平均律”。
“平均”最大的优点就是不管怎样移调或转调,都能够获得均等的音乐效果。这也是十二平均律优于纯律的地方。但这是相对的,因为十二平均律是将一个八度均分成12等分,所以每一个半音之间的震动比数都是一个除不尽的无限小数,所以无论演奏哪一个和弦都不可能得到真正完全谐和的音乐效果,只不过十二平均律影响的幅度相当小,比较之下仍是非常好的一个音程系统。 当前MIDI无法取代真人演奏效果的原因是因为真人演奏时演奏家会凭自己的耳朵判断音程和谐的程度,通常比较接近纯律,但在电脑中现时还无法更好做到,根本原因是音程定义系统上有着根本的差异,不过差异不太大。
五度相生律:以一音为基音,然后将频率比为3:2的纯五度音程作为生律要素,分别向基音两侧同时生音。假如C为基音,按照五度相生原理向上可生出G、D、A、E、B,向下可生出F、降B、降E、降A、降D、降G,将连同基音在内的十二个音写在一个八度之内。如下图所示[4]:
在西方,早在公元前6世纪古希腊哲学家、科学家毕达哥拉斯及其学派就提出了“五度相生律”,因此,五度相生律又被称为“毕达哥拉斯律”。毕达哥拉斯及其学派认为宇宙和谐的基础是完美的数的比例,音乐与宇宙天体存在类似。认为弦长比分别为2:1、3:2、4:3时发出相隔纯八度、纯五度、纯四度的音程定为完美的协和音程。他们将纯五度作为生律要素,由此产生“五度相生律”。
小提琴作为弓弦乐器, 其G、D、A、E四根弦从低到高就是以按五度定弦的。其中的A 音是标准音高440Hz。空弦拉动时A弦跟E弦是纯五度关系,而D弦与A弦也是纯五度关系,G与D弦也是纯五度关系。
十二平均律的数学原理
前面已经介绍过,十二平均律是将一个音程纯平均分成十二个均等的部分——半音。那为什么是十二呢?
声波振动的频率增加一倍,音调听起来就高一个八度。十二平均律将这个两倍的频率划分成了12份,也就是一个小二度的频率比是$\sqrt [12] {2}$,所以五度的频率比就是$2^{\dfrac {7}{12}}\simeq 1.498$. 与纯律的纯五度频率比$3:2$非常接近,人耳几乎听不出来差别。前面也说过,纯五度人耳听起来非常和谐。
当我们按照五度相生律划分音程时,从1开始,首先得到频率比$3/2$的G音。由G音,得到跟G音频率比为$3/2$的$\left( 3/2\right) ^{2}$这个音,当然这已经是下一个八度音程里的音了,对应到这个音程的音频率比应该是$\dfrac {\left( 3/2\right) ^{2}}{2}$,即为D. 重复这一过程,就会的到频率比为$\dfrac {\left( 3/2\right) ^{3}}{2}$的A,然后是$\dfrac {\left( 3/2\right) ^{4}}{2^{2}}$的E,$\dfrac {\left( 3/2\right) ^{5}}{2^{2}}$的B。当重复这个过程十二次时,$\dfrac {\left( 3/2\right) ^{12}}{2^{6}} \approx 2.01$。这个值已经非常非常接近于2。也就是说我们已经近似将频率比$1~2$这个范围划分出了12个半音。
在十二平均律里,因为五度的频率比与$3:2$接近,所以当钢琴按下C和G时,其发出的声音是非常和谐的。
音律关于振动的解释
————————————————————————
乐音的四个基本特性
人耳能听到的声音频率范围大约在 20Hz-20KHz之间,一般音乐的频率范围大致在 40Hz-15KHz 之间。
乐音有四种基本性质:音高(pitch)、音强(volume)、音长(duration)和音色(timbre),
又称作乐音四要素。与之相对应的客观物理量则分别是:频率(frequency)、声压(sound pressure)、时间(time)、频谱(spectrum)和波形(wave shape)。决定声音音高的主要是频率,而频谱则与音色关系最为密切。
音色主要决定于以下几个物理因素:谐波和分音的数目、谐波和分音的绝对强度和相对强度、谐波和分音的长短、分音的不协和程度、声音的基频、谐波和分音在听音区的位置等,它们组合的方式和量值的改变都会改变声波的波形,从而改变音色。 现代音乐声学中,对于音色的分析多采用频谱分析法,即通过声音的采集和分析系统把声音转化为可见的振动图像和频谱图像,再分析这些图像所代表的声音特征。声波振动图像直观反映声音随时间变化的特征,频谱图主要反映声音中分音数量与分音之间的强度关系。
基频与泛音、频谱分析
一段声波其实是由很多频率成分构成的。前面弹拨弦的振动公式也解释了这个问题,每种成分赋值大小都影响最后听到的音色是如何的,这些由琴的结构决定。
下图就是一个小提琴录音片段的频谱。从图中大概可以看到它的基频是440Hz左右,而其他的频率成分比如880Hz、1320Hz等等就是小提琴的泛音,这些泛音频谱分析就是将一段波形做傅立叶变换,得到不同频率成分的正弦波形的叠加,将声波信号以频谱的方式呈现。例如上图。利用频谱分析可以对声波进行有效的分析、叠加等操作。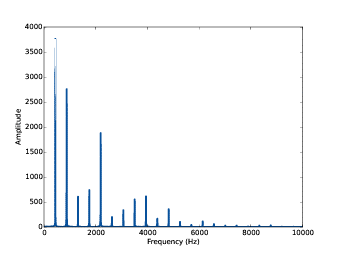
和谐
和谐是一个很抽象又不抽象的词。文章的前面也多次提到“和谐”,比如纯五度、纯八度、同度和谐。文字的描述只会感觉和谐这个概念很抽象,但是真正当你听到那些和谐的和弦,听到纯五度、纯八度,与小二度之间的对比,又很容易理解所谓的和谐的概念。这一小节就讨论“和谐”内在的理论基础。
首先是——拍——的概念。
在机械振动课上学过,在无阻尼单自由度简谐激励振动中,当激励频率与物体固有频率相近时,就会产生拍的现象。而二者频率相等时则会产生共振。在这里,讨论的“拍”指的是当两个频率相近的波叠加的时候产生的现象。
正弦函数的叠加公式如下:
$$ \sin u+\sin v =2\sin \dfrac {1}{2}\left( u+v \right) \cos \dfrac {1}{2}\left( u+v\right) $$
拿大二度叠加举例,假设是C和D叠加,其基频率分别为261.6Hz和294.3Hz。则有:
$$ \sin \left( 261.6\times 2\pi t\right) + \sin \left( 294.3\times 2\pi t\right) = 2sin \left( 555.9 \pi t\right)cos \left( 32.7 \pi t\right) $$
这个结果可以看成是$sin$函数的幅值按照$cos$函数的大小变化,也就是声波的幅值按照$cos \left( 32.7 \pi t\right) $变化,频率只有16.4Hz。一般来说,人耳对频率较低的声波变化是比较敏感的。这时候人耳能感受到的这种有规律的有强弱变化的声波,大概就是一种有“嗡嗡嗡”的声音,不是持续、明亮的乐音。
用Gragher做上述函数的图像,可以很直观地看出这种变化: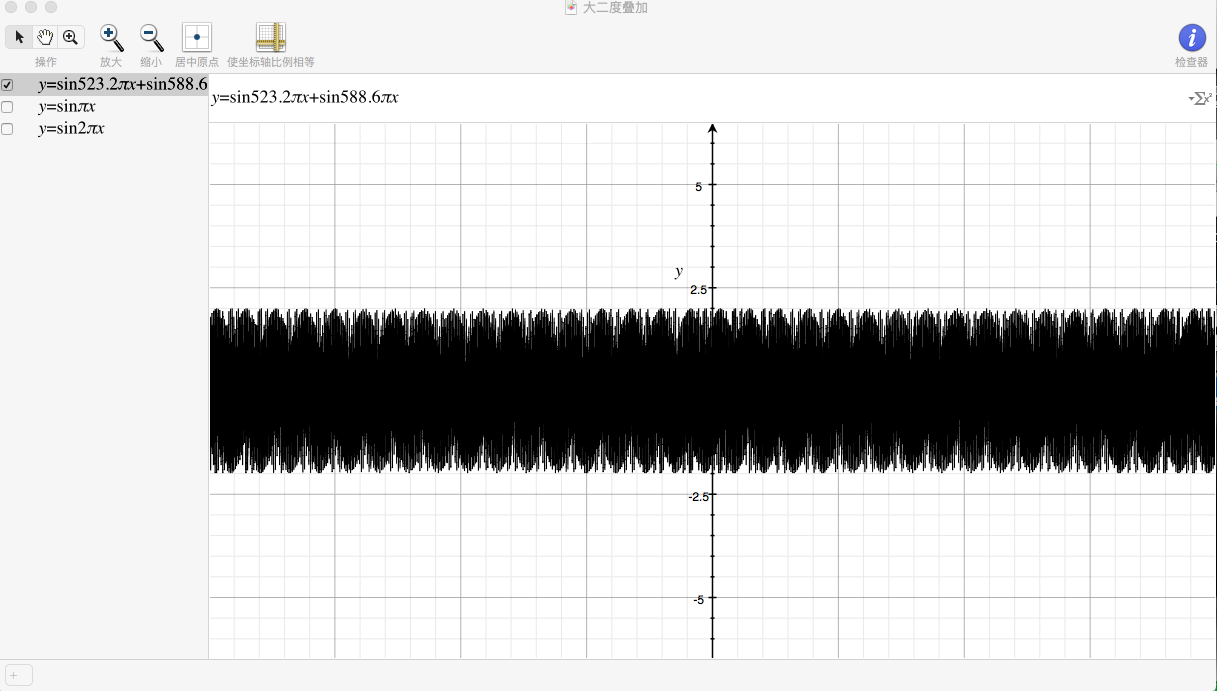
事实上,前面也解释过,当小提琴拉奏某个音的时候,其实人耳听到的不只有基频,还有各种泛音和分音。其叠加情况也跟基频类似,结果就是产生这种不和谐的拍现象。
而当纯五度的情况,就不会出现这种“拍”的现象。假设是同时拉奏C和G,那么简单的正弦函数叠加就是
$$ \sin \left( 261.6\times 2\pi t\right) + \sin \left( 392.5\times 2\pi t\right) = 2sin \left( 654.1 \pi t\right)cos \left( 130.9 \pi t\right) $$
图像为:
纯八度的叠加图像为:
就没有前面那种拍现象。
所以纯律的基础就是,当两个声波的频率比是简单的整数比,比如3:2、2:1时,比较容易得到频率仍旧很高的周期波。它们基频与泛音群的叠加,得到仍旧持续、响亮、和谐的声音。
小提琴的调音过程
————————————————————————
小提琴的调音方法,包括大提琴、低音提琴等,基本都常用双弦法调音。
首先,要学会调A弦(二弦),这时需要一个定音器——吹的(如单簧管)或者是电子的,在奏响定音器的A弦音后,在琴上以长弓拉响A弦,这时便会有两个声波同时进行:一个是定音器的A, 另一个是小提琴的A。
不准的A弦是不会和定音器的A音相和谐的。当定音器的A和不准的小提琴的A同奏响时,两个音这时应是一个同度的关系,可现在却是一种接近度的关系 所以在混合的两个音响中能分明地听见嗡嗡嗡的声音,这就表明小提琴上的弦是不准的,需要调高或调低。等到A弦的音准了后,琴的A音与定音器的A音同时奏响时就不会有嗡嗡嗡的声响。
有了A弦的标准音,就可以此为基础,继续调E和D弦了。之前提到过,小提琴的四根弦之间是纯五度关系。当D弦和准的A弦一同奏响时,两个音这时应是一个纯五度的关系,纯五度是与同度、八度一样和谐的双音,但在两个音响中能分明地听见”嗡嗡嗡”的声音时,这就表明弦是不准的,需要调高或调低。
当定音器的A音与小提琴的A弦同时奏响时,如果是此时小提琴的A弦是准的,则我们会听到一个和谐的双音。当A弦不准的时候,A弦发出的音跟定音器的A音频率相差不大,根据前面的分析,常常会产生拍的现象,也就是我们会听到不和谐的感觉。通过扭动弦轸以调整琴弦的松紧,改变其固有频率和音色。在小提琴音调准之后,我们会听到和谐的同度音。
在根据定准的A弦调节D弦的时候,因为它们之间是纯五度关系。而前面已经解释过,纯五度关系的两个音的频率比为3:2,是较小的整数比。他们之间波的叠加会产生相对规律的波,如前面的3:2纯五度正弦波叠加那样。我们听起来就非常和谐。根据同样的道理,可以校准其余的弦。
总结
————————————————————————
这次大作业,探究了小提琴的发声原理以及琴弦的振动模型,得到了影响琴弦固有频率的因素。用数学和振动相关知识解释了关于音律背后的理论依据,而且对小提琴调音过程中常提到的关于双音和谐做了简单的直观的解释。最后介绍了小提琴调音的过程,并根据前面探究过的纯五度和同度和谐以及调音操作做了详细的理论解释。
通过此次作业,对波的叠加、通过傅立叶变换进行的频谱分析、弦的振动分析都有了更加深刻的认识。特别是对于乐器的发声和调音原理、乐理背后的数学知识、对音乐直观感受背后的理论解释,都有了更深的理解。感受到了音乐背后的数学之美。
————————————————————————
参考文献及参考网站
- 图片来自维基百科https://zh.wikipedia.org/wiki/%E5%B0%8F%E6%8F%90%E7%90%B4
- 关于自激振动相关的解释、概念来自于《机械振动》,张义民编著,清华大学出版社
- 参考自《小提琴弦振动与琴体腔谐振研究》,贾雄
- 图片来自于百度百科http://baike.baidu.com/view/41790.htm
- 图片来自于https://gist.github.com/rickyteng/f8612146cb6ba9f717b5,《Sounds and signals,第一章》