聚类算法的最优k值选择

为了解决之前那个道路分割问题的有序数据聚类算法的k值确定问题，查阅了一些在聚类问题中确定最优k值的资料。
之前在学习吴恩达《机器学习》课程的时候，有介绍关于确定聚类算法中一个简单的确定k值的方法——手肘法。用不同的k值进行聚类，计算误差平方和。显然，随着k的增大，误差平方和必然减小：


在这个类似于手肘的图中，肘关节对应的k值就是我们认为对于此问题最合适的k值。小于该k值误差平方和太大，而大于该k值对降低误差平方和的作用不大、且会使类间的相似度太大。
不过根据数据特征的不同，也会存在肘点不明显的情况。该方法简单直接，不过需要绘图后判断，肘点的确定没有量化的公式和标准。对于该道路分割问题，想要得到的解为根据道路的起伏程度自适应选择最佳分类数目和分类结果。所以手肘法在此问题中不能满足需求。

介绍一下问题定义：

假设数据样本为$x_1, x_2, x_3,…,x_n$, 需要将这$n$条数据分为$k$类，这个分类问题记为$p(n,k)$。其中的某一类用$G_{ij}$表示，该类内包含的数据范围为$x_i,x_{i+1},…,x_{j}$。
定义类内的直径$D_{ij}$
$$ D_{ij} = \sum ^{j}_{l=i}\left|\left| x_{l}-\overline {x_{ij}}\right|\right| _{2} $$
其中$x_{ij}$为类$G_{ij}$的中心点：
$$ \overline {x_{ij}}=\left(j-i+1\right) \sum ^{j}_{l=i}x_{l} $$
所谓的类内直径，也就是类内各点到中心点的欧氏距离之和。
最优分割的目标是使各个类内直径之和最小，记目标函数为$e[p(n,k)]$。分割点为$i_1,i_2,…,i_k$：
$$ e[p(n,p)]=\sum ^{k}_{j=1}D\left( i_j,i_{j+1}-1\right) $$
而最优的分割方案，就是求解使上述目标函数值最小的分割点组合。

关于自适应确定k值的算法

————————————————————————
可惜的是，在搜索了一些资料后，没有找到一个能够满足需求的根据数据特征自适应确定k值的算法。不需要直接指定k值的算法有很多，比如基于密度的聚类算法，或是基于山峰函数的减法聚类，Affinity Propagation(AP)聚类等等。这些算法虽然不需要直接指定聚类数目k，但是均需要指定k的超参数。

层次聚类算法仍旧是需要设定截止的层次，或者类内的差异阈值，经过几次实验时候，发现对于该问题由于诸多方面的原因无法得到很好的效果。

所以决定还是使用类似手肘法的方法，计算设定k值范围内所有分类的指标，选取指标最优的分类方法。

Gap Statics

————————————————————————
为了解决前文提过通过找肘点来找到最佳聚类数、但是肘点的选择标准不清晰的问题，斯坦福大学的Robert教授等提出了Gap Statistic来提供最优的k。
$D_{r}$表示在某k值下类r内任意两点的距离之和：
$$
D_{r}=\sum_{l=i_r}^{i_{r+1}-1} \sum_{l^{\prime}=i_r}^{i_{r+1}-1}||x_l-x_l^{\prime}||_{2}
$$
标准化后：
$$
W_{k}=\sum_{r=1}^{k}\left(\frac{1}{2\left(i_{r+1}-i_{r}\right)} D_{r}\right)
$$
$W_k$这个指标类似于误差平方和，一般来说需要找到$W_k$的肘点，而Gap Statistic方法则定义了间隔量Gap。
定义间隔量$\operatorname{Gap}_n(k)$为：
$$
\begin{aligned}
\operatorname{Gap}_n(k) &= E_n^{*} { \log (W_k) } -\log (W_k) \\
&=\frac{1}{B} \sum_{b=1}^B \log (W_{kb}^{*}) - \log (W_k)
\end{aligned}
$$
式中$E_n^{*}{ \log (W_k) }$为${ \log (W_k) }$的参考分布(由蒙特卡洛模拟得到)在n个样本下的期望。即在样本所在的空间（该空间的范围即为样本的范围），按照均匀分布产生与样本数目n同样多的随机样本，对产生的新的样本进行聚类（在该有序样本聚类中采用了最优分割法，代码中展示的亦是如此）。该过程重复B次，求平均值即可求得该期望值。B的取值一般为20，B取得过大会导致计算量的增多，但对结果的影响却有限。
$Gap(k)$实际上是衡量了$W_k$和$W_k$的期望之间的差异，$Gap(k)$最大值对应的点就是$W_k$与其期望差异最大的点，对应的k值就是最佳聚类数。下图是Robert论文里的一个聚类示例的指标的计算结果：

从图d中可以看得出来，最优的聚类数目为2。
Robert还在论文里提出了method b：计算标准差$sd_k$：
$$
\operatorname{sd}(\mathrm{k})=\sqrt{\frac{1}{B} \sum_{\mathrm{b}}\left(\log \mathrm{W}_{\mathrm{kb}}^{*}-\frac{1}{B} \sum_{b=1}^{B} \log \left(W_{k b}^{*}\right)\right)^{2}}
\\
\mathrm{s}_{\mathrm{k}}=\sqrt{\frac{1+\mathrm{B}}{\mathrm{B}}} \operatorname{sd}(\mathrm{k})
$$
选择满足$Gap(k)>=Gap(k+1)−s(k+1)$的最小的k作为最优的聚类个数。对于该有序数据的聚类问题，参考代码如下：

% Gap Statistic
% Author: Zhai
% Date: 2019/12/6
%------------------------------%
clear
load data

l = 4; %单段限制长度。
n = length(s);

B = 20;
minC = 1; 
maxC = 30;
D = zeros(maxC,1);
ED = zeros(maxC,B);
Gap = zeros(maxC,1);
omega  = zeros(maxC,1);
s  = zeros(maxC,1);

tic

for k=minC:maxC
    p = zeros(n,k); %存储分类点的索引
    e = 1e6*ones(n,k); %初始化cost存储矩阵

    e_tmp = 1e6*ones(n,1);

    for gs = 1:B+1
    
        if gs == B+1
            x = g;
        else
            x = min(g) + (max(g)-min(g)).*rand(n,1);
        end

        for i = (l*k-(l-1)):(n-l*(k-k+1)+1)
            center = sum(x(i:n))/(n-i+1)*ones(n-i+1,1);
            e(i,k) = sum(abs(x(i:n)-center));
        end

        for j=k-1:-1:1
            for i=(l*j-(l-1)):(n-l*(k-j+1)+1)
                for u=(i+l):(n-l*(k-j)+1)
                    center = sum(x(i:u-1))/(u-i)*ones(u-i,1);
                    e_tmp(u) = sum(abs(x(i:u-1)-center)) + e(u,j+1);
                end	
                e(i,j) = min(e_tmp((i+l):(n-l*(k-j)+1)));
            end
        end

        if gs == B+1
            D(k) = e(1,1);
        else
            ED(k,gs) = e(1,1);
        end

    end

    omega(k) = sum(log(ED(k,:)))/B;
    Gap(k) = omega(k)/B-log(D(k));
    s(k) = sqrt((1+B)/B)*sqrt(sum((log(ED(k,:))-omega(k)).^2)/B);	
end

delta = zeros(maxC-1,1);
for k = 1:maxC-1
    delta(k) = Gap(k)-(Gap(k+1)-s(k+1));
end

for k = 1:100
    if Gap(k)>(Gap(k+1)-s(k+1))
        break
    elseif k>=maxC
        break
    end
end

toc

optimalK = k;
figure(1);
plot(Gap);
figure(2);
bar(delta)

method b结果如图所示，故最优的k选择为6：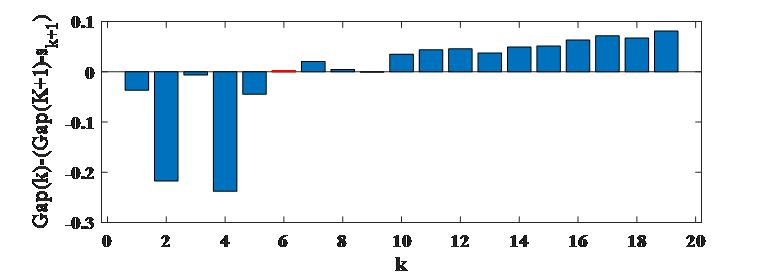

SilhouetteCoefficient（轮廓系数）

————————————————————————
轮廓系数比较简单，轮廓系数是类的密集与分散程度的评价指标。
将待分类数据聚为n个簇之后。对于每个点i，分别计算它们的轮廓系数：
计算 a(i) = average(i到所有它属于的簇中其它点的距离)
计算 b(i) = min(i到与它相邻最近的一簇内的所有点的平均距离)
那么i的轮廓系数就为：
$$
S(i)=\frac{b(i)-a(i)}{\max {a(i), b(i)}}
$$
对该有序聚类问题的参考代码为：

% SilhouetteCoefficient
% Author: Zhai
% Date: 2019/12/6
%------------------------------%
clear
figure;
load data

l = 2;%单段限制长度。
n = length(x);

minC = 1; 
maxC = 20;
h = minC:maxC;
D = zeros(maxC,1);

tic
sc = zeros(length(h),1);
for k=h
p = zeros(n,k); %存储分类点的索引
e = 1e6*ones(n,k); %初始化cost存储矩阵

e_tmp = 1e6*ones(n,1);

for i = (l*k-(l-1)):(n-l*(k-k+1)+1)
    center = sum(x(i:n))/(n-i+1)*ones(n-i+1,1);
    e(i,k) = sum(abs(x(i:n)-center));
end

for j=k-1:-1:1
    for i=(l*j-(l-1)):(n-l*(k-j+1)+1)
        for u=(i+l):(n-l*(k-j)+1)
            center = sum(x(i:u-1))/(u-i)*ones(u-i,1);
            e_tmp(u) = sum(abs(x(i:u-1)-center)) + e(u,j+1);
        end
        [e(i,j),t] = min(e_tmp((i+l):(n-l*(k-j)+1)));
        p(i,j) = i+l-1+t;
    end
end

opt_point = zeros(k,1);
opt_point(1) = 1;

for j=2:k
    opt_point(j) = p(opt_point(j-1),j-1);
    opt_point(j) = opt_point(j)-1;
end
opt_point(k+1) = n;

idx = zeros(n,1);
for j=1:k
    idx(opt_point(j):opt_point(j+1)-1) = j;
end
idx(end) = k;

s = zeros(n,1);
for pts = 1:n
    us = x(idx==(idx(pts)));
    if idx(pts)==1
        neigh1=1e6;
        neigh2=x(idx==(idx(pts)+1));
    elseif idx(pts)==k
        neigh1=x(idx==(idx(pts)-1));
        neigh2=1e6;
    else
        neigh1=x(idx==(idx(pts)-1));
        neigh2=x(idx==(idx(pts)+1));
    end
    us_len = length(us);
    neigh1_len = length(neigh1);
    neigh2_len = length(neigh2);
    
    a = mean(abs(x(pts)*ones(us_len,1)-us));
    b1 = mean(abs(x(pts)*ones(neigh1_len,1)-neigh1));
    b2 = mean(abs(x(pts)*ones(neigh2_len,1)-neigh2));
    b = min(b1,b2);
    s(pts) = (b-a)/max(b,a);    
end
sc(k) = mean(s);
end
sc(1) = 0;
toc

plot(sc)