模型预测控制（Model Predictive Control, MPC）作为一种非常有效的控制方法被应用于车辆的横纵向控制中（例如自适应巡航、车道保持等等低级别自动驾驶功能，或高级别自动驾驶的主动换道、规划路径跟踪控制）等等，其可以很好地处理各种复杂的约束。
不过现在量产车的L2级别的自动驾驶的底层控制算法应该是使用的PID和LQR。前段时间在某车企的面试中，跟面试官讨论过一些关于MPC算法在求解的时候由于涉及大规模的矩阵运算，故对计算性能要求较高等问题，而当前量产L2级别的自动驾驶车辆并没有高性能的运算能力，不知道工业界是否会在具有更高运算能力的L3上使用MPC替代LQR+PID。
模型预测控制的原理倒不是很难理解，但是从前期的系统建模、到后期的运算求解，涉及的内容比较多，故对这方面的学习内容进行了总结整理。主要参考数目列在文章最后的参考文献中。
示例模型介绍
————————————————————————
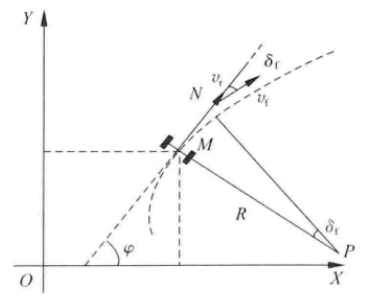示例为车辆轨迹跟踪控制中所使用的车辆运动学模型$\dot \xi = f\left( {\xi ,u} \right)$，此模型比较简单，无需说明复杂的建模原理，且此模型为非线性模型，可以完整说明MPC是如何应用于车辆轨迹跟踪控制中的。根据车辆运动学原理可对运动建模如式（1）。
$$
\left[\begin{array}{c}{\dot{X}} \\ {\dot{Y}} \\ {\dot{\varphi}}\end{array}\right]=\left[\begin{array}{c}{\cos \varphi} \\ {\sin \varphi} \\ {\tan \delta_{f} / l}\end{array}\right] v
\tag{1} $$
确定模型的状态量为$\xi=\left[\begin{array}{lll}{X,} & {Y,} & {\varphi}\end{array}\right]^{T}$, 模型的控制量为前轮偏角$u=\left[\begin{array}{ll}{v,} & {\delta_{f},}\end{array}\right]^{T}$。
非线性系统线性化方法
————————————————————————
通过运动学建模知识得到的系统模型(1)为一个非线性系统，无法直接用于线性时变模型预测控制，所以若用于MPC的系统模型为非线性系统，需要首先进行非线性系统的线性化处理。泰勒展开作为一种被广泛运用的线性化方法，可以利用多项式很好地逼近非线性系统工作点处的真实值。
假设车辆参考系统在任意时刻的状态和控制量满足如下方程：
$$
\dot{\xi}_{ref}(k+1)=f\left(\xi_{ref}(k), u_{ref}\right)
\tag{2}$$
参考系统在工作点$\left( \xi_{ref},u_{ref} \right)$进行泰勒展开，忽略高阶项，只保留一阶项：
$$
\dot \xi = f\left( \xi_{ref},u_{ref} \right) + {J_f}(\xi )\left( \xi - {\xi _{ref}} \right) + {J_f}(u)\left( u - {u_{ref}} \right)
\tag{3}$$
${J_f}(\xi)$和${J_f}(u)$分别为f相对于$\xi$和$u$的雅可比矩阵。(3)-(2)则得到线性化之后的线性时变方程为：
$$
\dot {\tilde \xi} = A(t)\tilde \xi (t) + B(t)\tilde u(t)
\tag{4} $$
式中：$ \tilde \xi (t) = \xi - \xi_{ref},\quad \tilde u(t) = u - u_{ref} $, $A(t){\rm{ = }}{J_f}(\xi )$, $B(t){\rm{ = }}{J_f}(u)$
根据上述线性化方法，对式(1)分别对于$\xi $和$u$计算雅可比矩阵得：
$$
A=\left[\begin{array}{ccc}{0} & {0} & {-v \sin \varphi} \\ {0} & {0} & {v \cos \varphi} \\ {0} & {0} & {0}\end{array}\right], B=\left[\begin{array}{cc}{\cos \varphi} & {0} \\ {\sin \varphi} & {0} \\ {\frac{\tan \delta_{f}}{l}} & {\frac{v}{l \cos ^{2} \delta_{f}}}\end{array}\right]
\tag{5}$$
（雅可比矩阵是一阶偏导数以一定方式排列成的矩阵：）
$$
\left[\begin{array}{ccc}{\frac{\partial y_{1}}{\partial x_{1}}} & {\cdots} & {\frac{\partial y_{1}}{\partial x_{n}}} \\ {\vdots} & {\ddots} & {\vdots} \\ {\frac{\partial y_{m}}{\partial x_{1}}} & {\cdots} & {\frac{\partial y_{m}}{\partial x_{n}}}\end{array}\right]
$$
即可得到线性化系统：
$$
\begin{aligned}
&\left[\begin{array}{c}{\dot{x}-\dot{x}_{ref}} \\ {\dot{y}-\dot{y}_{ref}} \\ {\dot{\varphi}-\dot{\varphi}_{ref}}\end{array}\right]\\
=&\left[\begin{array}{ccc}{0} & {0} & {-v \sin \varphi} \\ {0} & {0} & {v \cos \varphi} \\ {0} & {0} & {0}\end{array}\right]\left[\begin{array}{c}{x-x_{ref}} \\ {y-y_{ref}} \\ {\varphi-\varphi_{ref}}\end{array}\right]+\left[\begin{array}{cc}{\cos \varphi} & {0} \\ {\sin \varphi} & {0} \\ {\frac{\tan \delta_{r}}{l}} & {\frac{v}{l \cos ^{2} \delta_{r}}}\end{array}\right]\left[\begin{array}{c}{v-v_{ref}} \\ {\delta_{f}-\delta_{ref}}\end{array}\right]
\end{aligned}
\tag{6}$$
模型离散化方法与代码实现
————————————————————————
连续模型需要经过离散化才能应用于模型预测控制器的设计，模型离散化的方法有很多，比如Tustin法，欧拉法等等。MATLAB的c2d函数也可以直接将连续系统转换为离散系统。
Tustin法是通过采用梯形近似的方法实现离散等价设计，采用Tustin法离散化的结果为：
$$ \begin{array}{l}
A_{k,t} = (I + TA(t)/2)(I - TA(t)/2)^{ - 1}\\
B_{k,t} = TB(t)
\end{array} $$
欧拉法则使用矩形进行近似，相对于Tustin法形式更简单，即最后一个周期内$e(t)$所包围的面积使用$Te(k - 1)$代替。对于系统$\begin{array}{l}
\dot x = A(t)x + B(t)u\\
y = Cx
\end{array}$，采用欧拉法离散化的结果为：
$$ \begin{array}{*{20}{l}}
A_{k,t} = I + TA(t)\\
B_{k,t} = TB(t)
\end{array} $$
（I为单位矩阵，T为离散步长）。系统（4）离散化之后的结果为：
$$ \tilde \xi (k + 1) = A_{k,t}\tilde \xi (k) + B_{k,t}\tilde u(k) \tag{7} $$
$$
A_{k, t}=I+T A(t)=\left[\begin{array}{ccc}{1} & {0} & {-v \sin \varphi T} \\ {0} & {1} & {v \cos \varphi T} \\ {0} & {0} & {1}\end{array}\right], \quad B_{k, t}=T B(t)=\left[\begin{array}{cc}{\cos \varphi T} & {0} \\ {\sin \varphi T} & {0} \\ {\frac{\tan \delta_{f} T}{l}} & {\frac{v T}{l \cos ^{2} \delta_{f}}}\end{array}\right]
$$
观测方程:
$$ \eta (k) = C_{k,t},\tilde \xi (k) \tag{8} $$
$$ C_{k,t} = \left[ \begin{array}{*{20}{c}}
1&0&0\\
0&1&0\\
0&0&1
\end{array} \right] $$
系统参数初始化：1
2
3
4
5
6
7
8
9
10
11
12
13Nx=3;%状态量的个数
Nu =2;%控制量的个数
Np =60;%预测步长
Nc=30;%控制步长
Row=10;%松弛因子
t_d =u(3)*pi/180;%CarSim输出的为角度，角度转换为弧度
%半径为25m的圆形轨迹,速度为5m/s
r(1)=25*sin(0.2*t);
r(2)=25+10-25*cos(0.2*t);
r(3)=0.2*t;
vd1=5;
vd2=0.104;
L = 2.6;
MATLAB S-Funtion中，初始化状态矩阵的代码为：1
2
3
4
5
6
7
8T=0.1;
a=[1 0 -vd1*sin(t_d)*T;
0 1 vd1*cos(t_d)*T;
0 0 1];
b=[cos(t_d)*T 0;
sin(t_d)*T 0;
tan(vd2)*T/L vd1*T/(L*cos(vd2)^2)];
c=[1 0 0; 0 1 0; 0 0 1];
模型增量形式转换与预测方程
————————————————————————
在接下来的目标函数设计的过程中，用控制增量取代控制量并加入松弛因子，可以对控制增量进行直接限制，也能防止执行过程中没有可行解的情况。故需要将系统（7）转换为控制增量的形式。
设定新的状态变量为$\hat \xi (k|t) = \left[ \begin{array}{*{20}{l}}
\tilde \xi (k|t)\\
{u(k - 1|t)}
\end{array} \right]$。将上一时刻的控制变量添加入状态变量，控制增量作为新的控制变量。新的状态空间表达式为：
$$
\begin{array}{l}{\hat{\xi}(k+1 | t)=\tilde{A}_{k, t}, \hat{\xi}(k | t)+\tilde{B}_{k, t} \Delta u(k | t)} \\ {\eta(k | t)=\tilde{C}_{k, t}, \hat{\xi}(k | t)}\end{array}
\tag{8} $$
根据控制量与控制增量的关系可得：
$$
\begin{array}{l}
\tilde \xi (k + 1|t) = {A_{k,t}}\tilde \xi (k|t) + {B_{k,t}}[u(k - 1|t) + \Delta u(k|t)]\\
u(k|t) = u(k - 1|t) + \Delta u(k|t)
\end{array}
\tag{9}$$
则对应的$A_{k,t},B_{k,t}$矩阵会相应地变为$\tilde A_{k,t},\tilde B_{k,t}$：
$$
\begin{aligned}
&\tilde{A}_{k, t}=\left[\begin{array}{ccc}{A_{k, t}} & {B_{k, t}} \\ {0_{m \times n}} & {I_{m}}\end{array}\right], \quad \tilde{B}_{k, t}=\left[\begin{array}{c}{B_{k, t}} \\ {I_{m}}\end{array}\right] \\
&\tilde{C}_{k, t}=\left[\begin{array}{cc}{C_{k, t}} & {0}\end{array}\right]
\end{aligned}
\tag{10} $$
增量形式转换的代码为：1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17kesi=zeros(Nx+Nu,1);
kesi(1)=u(1)-r(1);
kesi(2)=u(2)-r(2);
kesi(3)=t_d-r(3);
kesi(4)=U(1);
kesi(5)=U(2);
A_cell=cell(2,2);
B_cell=cell(2,1);
A_cell{1,1}=a;
A_cell{1,2}=b;
A_cell{2,1}=zeros(Nu,Nx);
A_cell{2,2}=eye(Nu);
B_cell{1,1}=b;
B_cell{2,1}=eye(Nu);
A=cell2mat(A_cell);
B=cell2mat(B_cell);
C=[1 0 0 0 0;0 1 0 0 0;0 0 1 0 0;];
若已知t时刻的系统状态量$\hat \xi (k|t)$和控制增量$\Delta u(k|t)$，则可通过式(8)计算下一时刻系统的输出量$\eta (k + 1|t)$，不断迭代计算，则可获得预测时域内的系统输出量。如果系统的预测时域为 Np，以下公式使用P 表示；控制范围为Nc，以下公式中使用 N表示。通常，控制器的控制范围不超过其预测范围，即N ≤ P。为进一步降低模型预测控制算法的复杂程度，假设在预测时域内的时变系统的矩阵不变，与当前时刻矩阵相同。即：
$$ \begin{array}{*{20}{l}}
{A_{k,t} = {A_t},k = t, \cdots t + P}\\
{B_{k,t} = {B_t},k = t, \cdots t + P}\\
{C_{k,t} = {C_t},k = t, \cdots t + P}
\end{array} \tag{11} $$
由离散的系统状态方程迭代可以计算得到，P步内的系统输出：
$$
\begin{aligned}
&\eta (t + P|t) \\
= &{\tilde C_t}\tilde A_t^P\hat \xi (t|t) + {\tilde C_t}\tilde A_t^{P - 1}{\tilde B_t}\Delta u(t|t) + \cdots + {\tilde C_t}\tilde A_t^{P - N - 1}{\tilde B_t}\Delta u(t + N|t)
\end{aligned}
\tag{12} $$
为更清楚的看出预测时域内状态量、输出量和控制量之间的关系。对以上计算过程进行整理：
$$ Y(t) = {\Psi _t}\hat \xi (t|t) + {\Theta _t}\Delta U(t) \tag{13} $$
其中系统预测输出和输入序列分别为：
$$
Y(t)=\left[\begin{array}{c}{\eta(t+1 | t)} \\ {\eta(t+2 | t)} \\ {\vdots} \\ {\eta(t+N | t)} \\ {\vdots} \\ {\eta(t+P | t)}\end{array}\right], \quad \Delta U(t)=\left[\begin{array}{c}{\Delta u(t | t)} \\ {\Delta u(t+1 | t)} \\ {\vdots} \\ {\Delta u(t+N | t)}\end{array}\right]
$$
系统预测矩阵分为：
$$
\Psi_{t}=\left[\begin{array}{c}{\tilde{c}_{f} \tilde{A}_{t}} \\ {\tilde{C}_{r} \tilde{A}_{t}^{2}} \\ {\tilde{c}_{r} \tilde{A}^{v}} \\ {\tilde{c}_{r} \tilde{A}_{t}^{v}}\end{array}\right], \quad \Theta_{t}=\left[\begin{array}{cccc}{\tilde{c}_{f, t}} & {0} & {0} & {0} \\ {\tilde{C}_{r} \tilde{A} \tilde{B}_{t}} & {\tilde{C}_{t} \tilde{B}_{t}} & {\cdots} & {0} \\ {\tilde{C}_{t} \tilde{A}^{-1} \tilde{B}_{t}} & {\tilde{C} A_{r}^{x-2} \tilde{B}_{t}} & {\cdots} & {\tilde{C}_{t} \tilde{B}_{t}} \\ {\tilde{C}_{r} \tilde{A}_{t}^{R-1} \tilde{B}_{t}} & {\tilde{C}_{r} \tilde{A}_{t}^{P-2} \tilde{B}_{t}} & {\cdots} & {\tilde{C}_{r} \tilde{A}_{t}^{R-N-1} \tilde{B}_{t}}\end{array}\right]
$$
预测方程建立的代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14PHI_cell=cell(Np,1);
THETA_cell=cell(Np,Nc);
for j=1:1:Np
PHI_cell{j,1}=C*A^j;
for k=1:1:Nc
if k<=j
THETA_cell{j,k}=C*A^(j-k)*B;
else
THETA_cell{j,k}=zeros(Nx,Nu);
end
end
end
PHI=cell2mat(PHI_cell);
THETA=cell2mat(THETA_cell);
目标函数、约束设置与二次规划标准形式转化
————————————————————————
模型预测设计可以计算预测域的系统状态，但是控制增量序列$\Delta U(t)$是未知的，如何设立合理的目标函数，在约束范围内求解控制增量序列$\Delta U(t)$，成为一个关键问题。对于路径跟踪控制器，目标是快速稳定地跟上参考路径，因此设计目标函数如下：
$$
\begin{aligned}
&J(\xi(t), u(t-1), \Delta U(t))\\
=&\sum_{i=1}^{P}||\eta(t+i | t)-\eta_{ref}(t+i | t)||_{Q}^{2}+\sum_{i=0}^{N-1}||\Delta u(t+i | t)||_{R}^{2}+\rho \varepsilon^{2}
\end{aligned}
\tag{14}$$
第一项是计算预测时域内，预测系统的状态输出量和参考系统参考量之间的偏差，反映了系统对参考轨迹的跟踪能力。第二项反映了对控制量的约束，即控制的平稳性。通过调节权重矩阵Q和R使得系统可快速稳定的跟上参考轨迹，绕过障碍物。由该系统是时变系统，不能保证在每个时刻都有最优解，因此在优化目标中加入松弛因子，避免出现无解的情况。式(14)是目标函数的一般形式。
控制量约束、控制增量约束、输出约束：
$$ \begin{array}{l}
{u_{\min }}(t + k)u(t + k){u_{\max }}(t + k),\quad k = 0,1, \cdots ,N\\
\Delta {u_{min}}(t + k)\Delta u(t + k)\Delta {u_{\max }}(t + k),\quad k = 0,1, \cdots ,N\\
{y_{\min }}(t + k)y(t + k){y_{\max }}(t + k),\quad k = 0,1, \cdots ,N
\end{array} \tag{15}$$
为了方便计算机求解，需要通过相应的矩阵变换，将(14)(15)转化为标准二次型，即二次规划（Quadratic Programming, QP）问题。MATLAB中QP求解的标准格式如下：
$$
\text{min} _{x} \frac{1}{2} x^{T} Hx+f^{T} x \text { such that }\left\{\begin{array}{c}{A \cdot x \leq b} \\ { Aeq \cdot x=beq} \\ { lb \leq x \leq ub}\end{array}\right.
$$
其中，H为正定的Hessian矩阵；A，b为控制变量的不等式约束矩阵；Aeq和beq为控制变量的等式约束矩阵；lb，ub分别为控制变量的上下限约束。
首先定义预测时域内输出量的偏差：
$$ E(t) = {\Psi _t}\hat \xi (t|t) - {Y_{ref}}(t) \tag{16} $$
其中参考值：$Y_{ref}(t) = \left[ \eta _{ref}(t + 1|t), \cdots {\eta_{ref}}(t + P|t) \right]$。
将(16)带入(14)，并经过相应的矩阵运算后，可以将(14)转换成相应的二次型：
$$
\begin{aligned}
&J(\hat \xi (t),u(t - 1),\Delta U(t)) \\
=&\left[\Delta U(t)^T,\varepsilon\right]{H_t}{\left[ \Delta U(t)^T,\varepsilon \right]^T} + {G_t}{\left[ \Delta U(t)^T,\varepsilon \right]^T} + {P_t}
\end{aligned}
\tag{17}
$$
其中：
$$
\begin{aligned}
&{H_t} = \left[ \begin{array}{cc}
{\Theta _t^T}{Q_e}{\Theta _t} + {R_e}&0\\
0&\rho
\end{array} \right]
\\
&{G_t} = \left[ \begin{array}{*{20}{c}}
{2E(t)^T}{Q_e}{\Theta _t}&0
\end{array} \right]
\\
&{P_t} = {E(t)^T}{Q_e}{E(t)}
\end{aligned}
$$
$Q_e$和$R_e$分别是权重矩阵Q和R的扩展形式：
$$
{Q_e} =
\left[
\begin{array}{cc}
Q_{P \times P}&0_{P \times P}& \cdots &0_{P \times P}\\
0_{P \times P}&Q& \cdots &0_{P \times P}\\
\vdots & \vdots & \ddots & \vdots \\
0_{P \times P}&0_{P \times P}&0_{P \times P}&Q
\end{array}
\right]_{P \times P}
$$
$$
{R_e} =
\left[
\begin{array}{cc}
R_{u \times u}&0_{u \times u}& \cdots &0_{u \times u}\\
0_{u \times u}&R& \cdots &0_{u \times u}\\
\vdots & \vdots & \ddots & \vdots \\
0_{u \times u}&0_{u \times u}&0_{u \times u}&R
\end{array}
\right]_{N \times N}
$$
$P_t$为常量，不需要优化故最终目标函数可写成：
$$
J(\hat \xi (t),u(t - 1),\Delta U(t)) = \Delta \tilde U(t){H_t}\Delta \tilde U{(t)^T} + {G_t}\Delta \tilde U{(t)^T}
\tag{18}$$
其中：
$$ \Delta \tilde U(t) = \left[ {\Delta U(t)^T,\varepsilon } \right]^T \tag{18.1}$$
目标函数二次型矩阵建立代码：1
2
3
4
5
6
7
8
9
10
11
12H_cell=cell(2,2);
H_cell{1,1}=THETA'*Q*THETA+R;
H_cell{1,2}=zeros(Nu*Nc,1);
H_cell{2,1}=zeros(1,Nu*Nc);
H_cell{2,2}=Row;
H=cell2mat(H_cell);
error=PHI*kesi;
f_cell=cell(1,2);
f_cell{1,1}=2*error'*Q*THETA;
f_cell{1,2}=0;
f=cell2mat(f_cell);
约束条件(15)也需要按照标准形式转化，约束(15.1)与(15.3)为不等式约束，约束(15.2)为控制变量的上下限约束，该问题不存在控制变量的等式约束。约束(15.1)需要转换成控制增量的形式，并与(15.2)一起进行矩阵变换，转换成 的形式。
控制量与控制增量的关系如下：
$$ u(t + k) = u(t + k - 1) + \Delta u(t + k)
\tag{19}$$
则在预测域内：
$$
\begin{aligned}
\left[ \begin{array}{cc}
u_{t|t}\\
u_{t + 1|t}\\
{…}\\
u_{t + N|t}
\end{array}
\right]& =
\left[
\begin{array}{cc}
u_{t - 1}\\
u_{t - 1}\\
u_{t - 1}\\
u_{t - 1}
\end{array}
\right] + \left[
\begin{array}{cc}
\Delta u_{t|t}\\
\Delta u_{t|t} + \Delta u_{t + 1|t}\\
{…}\\
\Delta u_{t|t} + \Delta u_{t + 1|t} + … + \Delta u_{t + N|t}
\end{array}
\right] \\
&={1_N} \otimes u_{t - 1} + {L_N} \otimes {I_u}\Delta U(t)
\end{aligned}
\tag{20}$$
其中，$1_N$为N维的元素为1的列向量，$L_N$为N维全1下三角矩阵，$I_u$为维度与控制变量维度相同的单位矩阵，$ \otimes $为克罗内克积。
（克罗内克积的运算规则为：）
$$
A \otimes B = \left[
\begin{array}{cc}
a_{11}B& \cdots &a_{1n}B\\
\vdots & \ddots & \vdots \\
a_{m1}B& \cdots &a_{mn}B
\end{array}
\right]
$$
所以约束(15.1)可以转换为：
$$
\begin{array}{l}
U_{\min }A\Delta {U_t} + U_{t - 1}U_{\max }\\
A = {L_N} \otimes {I_u}\\
U_{t - 1} = {1_N} \otimes u_{t - 1}
\end{array}
\tag{21.1}$$
约束(15.3)则为：
$$
Y_{\min } \le {\Psi _t}\xi (t|t) + {\Theta _t}\Delta U(t) \le Y_{\max }
\tag{21.2}$$
将(21.1)和(21.2)进行运算：
$$
\begin{array}{l}
A\Delta U_t \le U_{\max } - U_{t - 1} \\
- A\Delta U_t \le - U_{\min } + U_{t - 1} \\
\Theta _t \Delta U(t) \le Y_{\max } - \Psi _t \xi (t|t)\\
- \Theta _t \Delta U(t) \le - Y_{\min } + \Psi _t \xi (t|t)
\end{array}
\tag{22}$$
将(21)转换成矩阵的形式并结合(18.1)为：
$$ A_{cons}\Delta \tilde U_t \le b_{cons}
\tag{23}$$
$$
A_{cons} =
\left[
\begin{array}{cc}
A&0_{u \times N,u \times N}\\
-A&0_{u \times N,u \times N}\\
\Theta _t& \vdots \\
- \Theta _t&0_{u \times N,u \times N}
\end{array}
\right],
b_{cons} = \left[
\begin{array}{cc}
U_{\max} - U_{t-1} \\
-U_{\min} + U_{t-1} \\
Y_{\max} - \Psi _t \xi (t|t) \\
-Y_{\min} + \Psi _t \xi (t|t)
\end{array}
\right]$$
约束(15.2)则可以转换为(M为ε的上限)：
$$
\begin{array}{l}
lb \le \Delta \tilde U_t \le ub\\
lb = [\Delta U_{\min };0],ub = [\Delta U_{\max };M]
\end{array}
\tag{24} $$
不等式约束建立代码：1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27A_t=zeros(Nc,Nc);
for p=1:1:Nc
for q=1:1:Nc
if q<=p
A_t(p,q)=1;
else
A_t(p,q)=0;
end
end
end
A_I=kron(A_t,eye(Nu));
Ut=kron(ones(Nc,1),U);
umin=[-0.2;-0.54;];
umax=[0.2;0.332];
delta_umin=[0.05;-0.0082;];
delta_umax=[0.05;0.0082];
Umin=kron(ones(Nc,1),umin);
Umax=kron(ones(Nc,1),umax);
A_cons_cell={A_I zeros(Nu*Nc,1);-A_I zeros(Nu*Nc,1)};
b_cons_cell={Umax-Ut;-Umin+Ut};
A_cons=cell2mat(A_cons_cell);
b_cons=cell2mat(b_cons_cell);
M=10;
delta_Umin=kron(ones(Nc,1),delta_umin);
delta_Umax=kron(ones(Nc,1),delta_umax);
lb=[delta_Umin;0];
ub=[delta_Umax;M];
MATLAB二次规划问题求解
————————————————————————
在每一个控制周期内，求解以上目标函数，即可得到控制时域内的控制序列：
$$
\Delta U(t) =
\left[
\begin{array}{cc}
\Delta u(t|t) \\
\Delta u(t + 1|t) \\
\vdots \\
\Delta u(t + N - 1|t)
\end{array}
\right]
$$
控制序列的第一个元素作为实际控制增量，与上一个时刻的控制增量叠加，得
到本次控制周期的实际控制量：
$$ u(t) = u(t - 1) + \Delta u(t|t) $$
采用MATLAB的二次规划求解器对此问题进行求解，代码为：1
2
3
4
5
6
7
8options = optimset('Algorithm','interior-point-convex');
[X,fval,exitflag]=quadprog(H,f,A_cons,b_cons,[],[],lb,ub,[],options);
u_piao(1)=X(1);
u_piao(2)=X(2);
U(1)=kesi(4)+u_piao(1);
U(2)=kesi(5)+u_piao(2);
u_real(1)=U(1)+vd1;
u_real(2)=U(2)+vd2;
目标函数二次型标准形式处理
————————————————————————
在第五章的目标函数设置时，主要考虑了轨迹的跟踪性能和控制的平稳性，但是目标函数的定义不限于如此的形式。比如在ACC问题中，文献[2]提出的目标函数：
$$
\min _{\Delta u}J = \sum\limits_{k = 1}^p
\left\{
y_{t + k}^T Q_t y_{t + k} + \Delta u_{t + k}^T R_t^{\Delta u} \Delta u_{t + k} + u_{t + k}^T R_t^u u_{t + k} + \rho \varepsilon ^2
\right\}
\tag{25}$$
目标函数(25)比(14)多了一关于最小化控制量的项。因为在ACC问题中，控制量为主车加速度，但是需要保证车辆平稳运行，则需要保证车辆加速度尽可能小，为了稳定车辆操控和舒适度，同时又需要保证车辆的加速度变化率尽可能小，故较于一般的目标函数(14)，形式更为复杂。
故本章节对目标函数(14)增加了第三项，并详细给出了目标函数的标准二次型转换的过程，对各种形式的目标函数都可以进行灵活处理。
$$
\begin{aligned}
J(\xi (t),u(t - 1),\Delta U(t)) =& \sum\limits_{i = 1}^P || \eta (t + i|t) - \eta _{ref}(t + i|t) ||_Q^2 \\
&+\sum\limits_{i = 0}^{N - 1} ||\Delta u(t + i|t)||_{R_{\Delta u}}^2 \\
&+\sum\limits_{i = 0}^{N - 1} ||u(t + i|t)||_{R_u}^2 + \rho {\varepsilon ^2}
\end{aligned}
\tag{26}$$
第一项：
$$
\begin{aligned}
&{J_1}(\xi (t),u(t - 1),\Delta U(t))\\
=&\sum\limits_{i = 1}^P || \eta (t + i|t) - \eta _{ref} (t + i|t) ||_Q^2 \\
=&\left( \Psi _t \widehat \xi (t|t) + \Theta _t \Delta U(t) - Y_{ref}(t) \right)^T Q\left( \Psi_t \widehat \xi (t|t) + \Theta _t \Delta U(t) - Y_{ref} (t) \right) \\
=&\left( \Theta_t\Delta U(t) + E(t) \right)^T Q \left( \Theta_t \Delta U(t) + E(t) \right)\\
=&\left( \Theta _t\Delta U(t) \right)^T Q\left( \Theta _t\Delta U(t) \right) + 2E(t)^TQ \Theta _t\Delta U(t) + E(t)^TQE(t)\\
=&\Delta U(t)^T \left( \Theta ^TQ\Theta _t \right) \Delta U(t) + 2E(t)^TQ \Theta _t \Delta U(t) + E(t)^TQE(t)
\end{aligned}
\tag{27}$$
第二项：
$$
\begin{aligned}
&{J_2}(\xi (t),u(t - 1),\Delta U(t))\\
=&\sum\limits_{i = 0}^{N - 1} ||\Delta u(t + i|t)||_{R_{\Delta u}}^2 \\
=&\Delta U{(t)^T}{R_{\Delta u}}\Delta U(t)
\end{aligned}
\tag{28}$$
第三项($\Delta {U_t}$和$U(t)$的转换详细推导为第五章式(20))：
$$ \begin{aligned}
&{J_3}(\xi (t),u(t - 1),\Delta U(t))\\
=&\sum\limits_{i = 0}^{N - 1} ||u(t + i|t)_{R_u}||^2 \\
=&U(t)^T R_u U(t)\\
=&\left( A\Delta U_t + U_{t - 1} \right)^T R_u \left( A\Delta U_t + U_{t - 1} \right)\\
=&\Delta U(t)^T\left( A^T R_u A \right)\Delta U(t) + 2U_{t - 1}^T R_u A\Delta U(t) + U_{t - 1}^T R_u U_{t - 1}
\end{aligned}
\tag{29}$$
对其进行矩阵整理，即可化为标准的二次型：
$$
J(\hat \xi (t),u(t - 1),\Delta U(t)) = \Delta \tilde U(t){H_t}\Delta \tilde U{(t)^T} + {G_t}\Delta \tilde U{(t)^T}
\tag{30}$$
$$
\Delta \tilde U(t) = \left[ \Delta U(t)^T,\varepsilon \right]^T
$$
$$
\begin{array}{l}
H_t = \left[
\begin{array}{cc}
\Theta _t^TQ{\Theta _t} + {A^T}{R_u}A + R_{\Delta u}&0\\
0&\rho
\end{array}
\right]\\
G_t = \left[
\begin{array}{cc}
2E(t)^TQ{\Theta _t} + 2U_{t - 1}^T{R_u}A&0
\end{array}
\right]\\
P_t = E(t)^TQE(t) + U_{t - 1}^T{R_u}U_{t - 1}
\end{array}
$$
————————————————————————
这篇NOTE主要是对《无人驾驶车辆模型预测控制》一书中MPC算法过程及其代码的梳理，书中的知识章节之间比较分散，在学习过程中消化了有关知识与推导之后做了这个梳理；最后一小节为对某参考文献中提出的目标函数进行二次型的详细推导，展示了与原文中不同结构的目标函数的二次型转换过程。
整个过程中除了学习书中的算法原理与代码，入门MPC时帮助理解较大的资料链接也一并列入参考资料中。
文献2是在MATLAB官网下载的参考论文，应该也是MATLAB模型预测控制工具箱中的ACC模块内部的控制原理。参考资料3是MATLAB官网对其路径跟踪模块的详细说明，对问题的理解具备参考价值；除此之外MATLAB还有车道保持模块（横向控制）和ACC模块（纵向控制），路径跟踪模块则是对这二者的集成。参考资料4为MATLAB推出的关于MPC在车辆控制中的应用入门系列视频，介绍了MPC的原理等等，对MPC的入门理解具有帮助。
除此之外，Apollo的车辆控制MPC代码也非常具有学习价值。
参考资料：
- 龚建伟,姜岩,徐威等. 无人驾驶车辆模型预测控制[M]. 北京理工大学出版社, 2014.
- Takahama T, Akasaka D. Model Predictive Control Approach to Design Practical Adaptive Cruise Control for Traffic Jam[J]. International Journal of Automotive Engineering, 2018,9(3):99-104.
- Path Following Control System
- Understanding Model Predictive Control, Part 2: What Is MPC?